در ۱۳۲۸ خورشیدی، ریاضیدان هندی، Kaprekar، فرآیندی را ابداع کرد که به عملیات Kaprekar شهرت یافت. در این عملیات، ابتدا عددی ۴ رقمی بایستی انتخاب شود؛ با این شرط که تمام ارقام با یکدیگر یکسان نباشند (مثلا، انتخاب اعدادی مانند ۷۷۷۷ یا ۵۵۵۵ و … نقض شرط است). پس از انتخاب عدد، بایستی ارقام آن عدد را به صورت بزرگترین و کوچکترین عدد مرتب کنیم. مثلا، اگر عدد ۸۴۵۷ را انتخاب کردید، بزرگترین ترتیبش میشود: ۸۷۵۴ و کوچکترین ترتیب نیز میشود: ۴۵۷۸٫ سرانجام، بایستی این دو عدد را از یکدیگر کم کنیم تا عددی جدید به دست آید و این مرحله را تکرار کنیم.
عملیات سادهای است، اما Kaprekar متوجه موضوعی شگفتانگیز شد. اجازه دهید این عملیات را با عدد ۱۳۹۰ امتحان کنیم وقتی که به عدد ۶۱۷۴ رسیدیم و اگر بخواهیم عملیات را ادامه دهیم در هر خط دوباره به عدد ۶۱۷۴ میرسیم. اجازه دهید این بار با عددی دیگر، مثلا با ۶۵۱۷ این عملیات را بررسی کنیم.عملیات اندکی طولانیتر میشود اما باز به همان نتیجه رسیدیم؛ یعنی عدد ۶۱۷۴٫ اگر اعداد دیگر را نیز امتحان کنید همواره به ۶۱۷۴ خواهید رسید؛ این همان اتفاق عجیبی بود که Kaprekar آن را کشف کرد.
این عملیات حداکثر ممکن است ۷ مرحله تکرار شود. بیشتر اعداد ۴ رقمی بدون ارقام تماما یکسان (۲۱۲۴ عدد) سه مرحلهای به ۶۱۷۴ میرسند، پس از آن ۱۹۸۰ عدد ۷ مرحلهای به این نتیجه میرسند.
مشابه این نتیجهی منحصر به فرد تنها در اعداد سه رقمی تکرار شده است. بدین صورت که اگر همین عملیات را برای اعداد سه رقمی تکرار کنیم همواره به ۴۹۵ میرسیم.
------
منبع : http://hellibammath.blogfa.com/
برچسبها:
برای تشکیل و بدست آوردن سه تایی های فیثا غورسی می توان با جایگذاری به جای u و v مقادیری برای a و b و c بدست آورد .
a=2uv
b=u2-v2
c=u2+v2
( به شرط اینکه اولا u و v با هم برابر نبوده
و دوم نسبت به هم اول باشند 1= (u,v)
و سوم اینکه u>v باشد )
به عنوان مثال اگر به u=2 و v=1 بدهیم مقادیر a=4 و b=3 و c=5 را به ما می دهد که با می دانیم با توجه به رابطه فیثاغورس تشکیل یک مثلث قایم الزاویه را می دهد .
32+42=52
16+9=25
برچسبها:
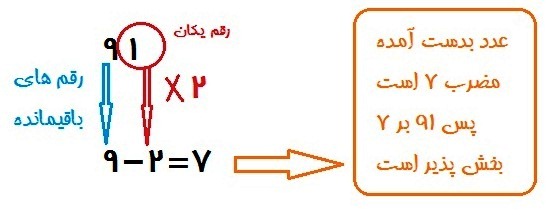
اگر یک عدد دو یا چند رقمی داشتیم برای بخش پذیری بر 7 ،
اول : رقم یکان را جداگانه در 2 ضرب می کنیم .
دوم : رقم های باقی مانده از همان عدد چند رقمی ( منظور به جز رقم یکان) را در نظر گرفته و از مقدار دو برابر رقم یکان ( قسمت قبل)کم می کنیم
سوم : اگر حاصل صفر شود یا عددی مضرب 7 بدست آید آن عدد بر 7 بخش پذیر است .
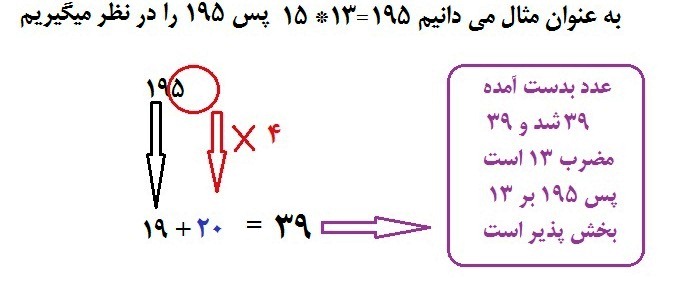
بخش پذیری بر 13 :
اول : رقم یکان را در نظر گرفته و آنرا 4 برابر می کنیم .
دوم : ارقام باقی ماندهاز آن عدد را با حاصل قسمت اول جمع می بندیم
سوم : اگر حاصل عددی مضرب 13 بدست آید آن عدد بر 13بخش پذیر است .
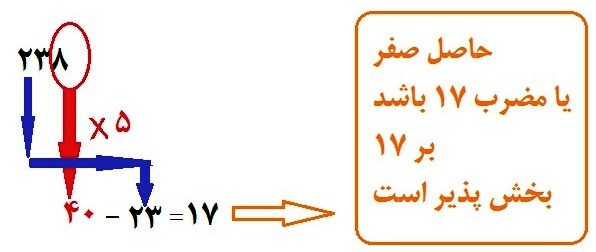
بخش پذیری بر 17:
اول : رقم یکان را در نظر گرفته و آنرا 5 برابر می کنیم .
دوم : سپس ارقام باقی مانده را از حاصل مرحله اول کم می کنیم
سوم : اگر حاصل صفر یا مضرب 17 باشد بر 17 بخش پذیر است
مثال : (می دانیم 238= 17*14 ) 238 را امتحان می کنیم داریم :
برچسبها:
محاسبه مجموع عددی در یک سری منظم
سری منظم : هر سری اعداد متوالی را که فاصله ی هر دو عدد متوالی آن ثابت باشد "سری منظم" می نامیم .
نکته 1 : در یک سری منظم میانگین اعداد برابر است با میانگین اولین و آخرین عدد ، یعنی جمع اوّلین و آخرین عدد تقسیم بر 2 .
نکته 2 : در یک سری منظم برای محاسبۀ تعداد عددها به این صورت عمل می کنیم : عدد آخر را منهای عدد اوّل کرده ، حاصل را بر فاصله ی متوالی دو عدد تقسیم کرده و با یک جمع می کنیم .
نکته 3 : مجموع اعداد برابراست با میانگین ضربدر تعداد .
مثال : حاصل 51 + ... + 15 + 11 + 7 + 3 را بدست آورید .
نکته 1 : 27 = 2 : (51+3 ) = میانگین
نکته 2 : 13 = 1 + 12 =1 + { 4 : (3-51) } = تعداد
نکته 3 : 351 = (27) .( 13 )= مجموع
منبع : http://ryazibijar.blogfa.com/
برچسبها:

 توجه: از این پس ، فایل های فشرده با حجمی بیش از ۱۰۰ مگابایت دارای ۵% ریکاوری هستند. این ویژگی باعث می شود تا مشکل در اکسترکت کردن فایل ها ، کاملا به صفر برسد. برای استفاده از این ویژگی ، اگر فایلی را دانلود کردید و با مشکل اکسترکت مواجه شدید ، نرم افزار Winrar را اجرا نموده ، به محلی که فایل های فشرده را دانلود کرده اید مراجعه کنید ، و تمامی پارت ها را انتخاب کرده و گزینه Repair که در قسمت بالایی نرم افزار موجود هست را بزنید. سپس محلی مناسب برای ذخیره سازی آن ها انتخاب کنید. پس از اتمام کار ، به محلی که برای ذخیره سازی انتخاب کردید مراجعه نموده و با آن فایل ها به اکسترکت بپردازید.
توجه: از این پس ، فایل های فشرده با حجمی بیش از ۱۰۰ مگابایت دارای ۵% ریکاوری هستند. این ویژگی باعث می شود تا مشکل در اکسترکت کردن فایل ها ، کاملا به صفر برسد. برای استفاده از این ویژگی ، اگر فایلی را دانلود کردید و با مشکل اکسترکت مواجه شدید ، نرم افزار Winrar را اجرا نموده ، به محلی که فایل های فشرده را دانلود کرده اید مراجعه کنید ، و تمامی پارت ها را انتخاب کرده و گزینه Repair که در قسمت بالایی نرم افزار موجود هست را بزنید. سپس محلی مناسب برای ذخیره سازی آن ها انتخاب کنید. پس از اتمام کار ، به محلی که برای ذخیره سازی انتخاب کردید مراجعه نموده و با آن فایل ها به اکسترکت بپردازید.
![]() دانلود در پارت های ۱گیگابایتی:
دانلود در پارت های ۱گیگابایتی:
دانلود پارت ۱ : Rapidshare Fileserve Duckload Sharehoster Direct Link
دانلود پارت ۲ : Rapidshare Fileserve Duckload Sharehoster Direct Link
دانلود پارت ۳ : Rapidshare Fileserve Duckload Sharehoster Direct Link
![]() برای دانلود به صورت پارت های ۲۰۰ مگابایتی از سرور Mediafire ، اینجا را کلیک کنید
برای دانلود به صورت پارت های ۲۰۰ مگابایتی از سرور Mediafire ، اینجا را کلیک کنید
![]() برچسب ها
برچسب ها
- دانلود با لینک مستقیم
- رمز:
- منبع :http://farsdesign.ir/?p=2004
برچسبها:
آنچه که میخوانید ریاضیات به سبک شیخ بهایی است که از کتاب خلاصة الحساب شیخ بهایی که در سال 1311 قمری نوشته شده به فارسی برگردانده شده است این کتاب شامل ده باب سی فصل در ریاضیات پایه ؛نجوم ؛وسیارات میباشد
در این روش؛در جمع چند عدد چند رقمی که زیر هم نوشته شده بجای آنک اعداد از سمت راست جمع زده شوند ,از سمت چپ جمع زده می شوند. مثلا:
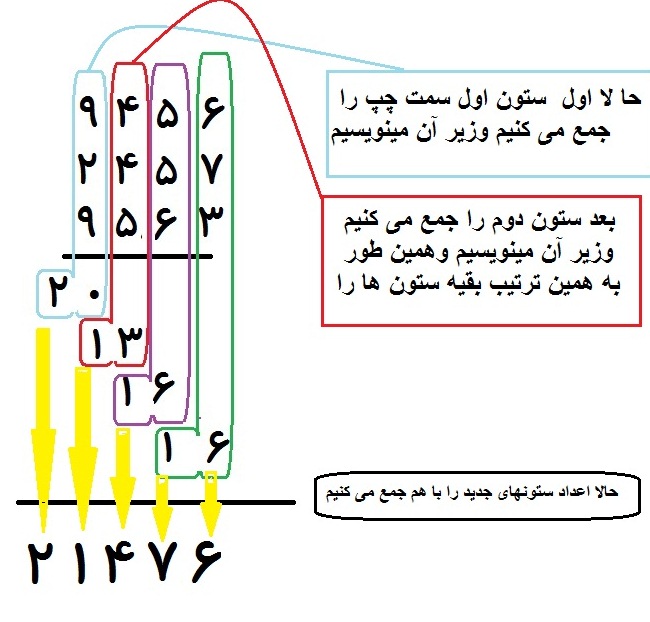
Normal 0 false false false EN-US X-NONE FA
همین طور که می بینید هیچ (ده بر یک یا بیست بر دو ویا...)بکار برده نمی شود وبرای یاد گیری خصوصا بچه ها بسیار راحت است
(با تشکر از آقای اسیری کرمانشاهی مدیر مسول گاهنامه پیام کر مانشاه)
برچسبها:
۲-این عدد را در ۵ ضرب کنید
۳-عدد بدست آمده را با تعداد روز های هفته (عدد ۷) جمع کنید.
۴-عدد بدست آمده را در ۴ ضرب کنید
۵-اکنون عدد بدست آمده را با عدد ۱۳ جمع بزنید
۶-عدد حاصل شده را در ۵ ضرب کنید
۷-چندم برج متولد شده اید ؟ عدد آن را به عددی که بدست آورده اید اضافه کنید
۸-عدد ۲۰۵ را از عدد بدست آمده کسر کنید
برچسبها:
در این ترفند ابتدا باید چند کار انجام بدهیم .
ابتدا روزهای هفته را به صورت زیر عدد گذاری می کنیم .
شنبه = ۰ یکشنبه = ۱ دوشنبه = ۲
سه شنبه = ۳ چهارشنبه = ۴ پنج شنبه = ۵
جمعه = ۶
سپس به سراغ یک تقویم می رویم و هفتمین روز از هر ماه را بدست به ترتیب عدد گذاری روزهای هفته در بالا شماره گذاری می کنیم .
مثلا ماههای سال ۸۹ به صورت زیر عدد گذاری می شود .
فروردین = ۰ (شنبه ) اردیبهشت = ۳ (سه شنبه ) خرداد = ۶
تیر = ۲ مرداد = ۵ شهریور = ۱
مهر = ۴ آبان = ۶ آذر = ۱
دی = ۳ بهمن = ۵ اسفند = ۰
سپس برای اینکه بدانیم فلان تاریخ چند شنبه است کافیست عدد داده شده را بر ۷ تقسیم کنیم و عدد باقیمانده را با عدد رمز همان ماه جمع کنیم . حاصل عددی است که متناظر با روز مورد نظر در همان ماه می باشد .
مثال ۱) ۲۳ آذرماه چند شنبه است ؟
کافیست ۲۳ را بر ۷ تقسیم کنیم که باقیمانده آن = ۲ بدست می آید . سپس عدد ۲ را با رمز متناظر با ماه آذر یعنی ۱ جمع می کنیم ۳ = ۱ +۲ . حاصل عدد ۳ می شود یعنی روز متناظر سه شنبه است .
نکته : ) گاهی اوقات وقتی عدد باقیمانده را با عدد رمز جمع می کنیم حاصل بزرگتر از ۶ می شود . که در این صورت باید دوباره حاصلجمع دو عدد باقیمانده و رمز را بر ۷ تقسیم کنیم . باقیمانده هرچه شد . جواب همان است .
مثال ۲ ) ۲۷ اردیبهشت ماه چند شنبه است ؟
وقتی ۲۷ را بر عدد ۷ تقسیم می کنیم ، باقیمانده ۶ بدست می آید . و هنگامی که عدد ۶ را با رمز مربوط به ماه اردیبهشت یعنی ۳ جمع می کنیم حاصل ۹ بدست می آید . ۹ = ۳+۶ که دوباره باید ۹ را بر ۷ تقسیم کنیم .
وقتی ۹ را بر ۷ تقسیم می کنیم ، باقیمانده ۲ بدست می آید . پس روز مورد نظر ما دوشنبه است .
مثال۳ ) ۱۳ بهمن چند شنبه است ؟
باقیمانده ۱۳ بر ۷ عدد ۶ است . و وقتی ۶ را با عدد رمز یعنی۵ جمع می کنیم حاصل ۱۱ می شود . و پس از تقسیم دوباره ۱۱ بر ۷ باقیمانده ۴ بدست می آید پس روز مورد نظر ۴ شنبه است .
برچسبها:

